The 2023 Distinct Distances Project
This is a brief introduction to the 2023 Polymath Jr project that will be run by Eyvi Palsson and Adam Sheffer. It concerns the famous distinct distances problem of Erdős.
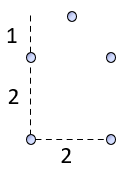
Consider this set of five points:
Every pair of points span a distance. When checking all pairs, we get that the distances spanned by this set are {√2, 2, √5, √10}. This is the set of distinct distances. It does not matter how many times each distance appears - only that it appears at least once.
The five vertices of a regular pentagon only span two distances:
Erdős was interested in much larger sets of points. For a huge n, he asked for the minimum number of distinct distances that can be spanned by n points. For example, n equally spaced points on a line span exactly n-1 distances.
Erdős arranged n points so that they spanned about n/√(log n) points. He conjectured that this is the best possible. This has led to a huge body of work, spanning many decades, and deep mathematical theories.
In the current Polymath Jr project, we return to small sets of points. Let g(k) be the maximum number of points that span exactly k distances. For example:
-
g(1)=3 since the three vertices of an equilateral triangle span only one distance. A set of four points cannot span only one distance.
-
g(2)=5, as demonstrated by the above regular pentagon. A set of six points cannot span only two distances.
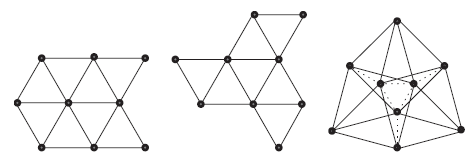
Three different ways for 9 points to span only four distances:
In this project, we will continue to explore the g(k) problem. A few potential approaches:
-
The largest value that is currently known is g(6)=13. We could work towards proving g(7).
-
Participants could search for larger configurations that span few distances, either by hand or using a computer.
-
Derive more general bounds for every k.
-
More experienced participants could try applying more modern techniques to this problem (we have some specific ideas for such techniques).
-
Anything else - go wild!
For additional reading, see:
-
We will provide a lot more material, but for that you'll have to join the project!